Leonardo Pisano, también conocido como Fibonacci, fue un famoso matemático italiano que difundió por Europa el sistema de numeración árabe (1, 2, 3...) con base decimal y con un valor nulo (el cero). Pero el gran descubrimiento de Fibonacci fue la Sucesión de Fibonacci que, posteriormente, dió lugar a la proporción áurea.
¿Qué es la Sucesión de Fibonacci? Se trata de una serie númerica: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, etc. Es una serie infinita en la que la suma de dos números consecutivos siempre da como resultado el siguiente número (1+1=2; 13+21=34). La relación que existe entre cada pareja de números consecutivos (es decir, si dividimos cada número entre su anterior) se aproxima al número áureo (1,618034) que se identifica con la letra Phi (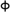
) del abecedario griego.
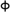) del abecedario griego.Bien, pues apliquemos todo esto al mundo visual. Creemos un rectángulo cuyos lados midan dos de los números de la serie de Fibonacci:
Y ahora vamos a dividirlo siguiendo la serie numérica:
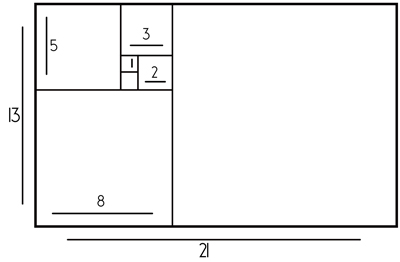
Si dibujamos una línea que una todos estos pequeños recuadros, quedaría algo parecido a esto:
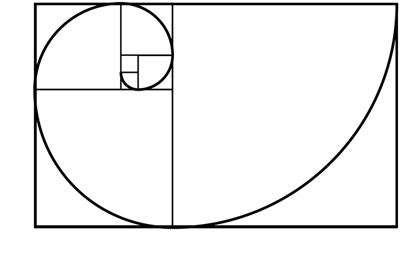
La espiral resultante (conocida como Espiral de Oro o Espiral Aurea) está permanentemente presente en la naturaleza: en las semillas de un girasol, en las conchas marinas...
La Relación entre la Regla de los Tercios y la Proporción Áurea
Lo que hacemos ahora es colocar cuatro espirales en el mismo rectángulo. Colocándolas de manera que se inicie una espiral en cada una de las cuatro esquinas del recuadro:
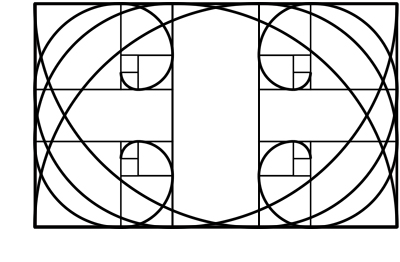
Qué, ¿te suena lo que ves? Vamos a marcar en rojo el centro de las espirales:
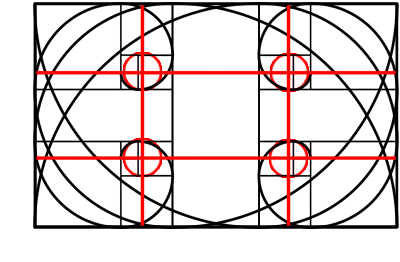
La regla de los tercios es una versión de la proporción áurea; en general, resulta más sencillo componer una imagen con la regla de los tercios en mente (o superpuesta en la pantalla de la cámara a modo de guía) que con la Espiral Áurea.
No hay comentarios:
Publicar un comentario